Your Graph brrhz problem definition images are available. Graph brrhz problem definition are a topic that is being searched for and liked by netizens now. You can Get the Graph brrhz problem definition files here. Find and Download all royalty-free vectors.
If you’re searching for graph brrhz problem definition images information related to the graph brrhz problem definition interest, you have come to the ideal site. Our site always gives you suggestions for downloading the highest quality video and image content, please kindly hunt and locate more enlightening video articles and images that fit your interests.
Graph Coloring Problem Definition. Is there a proper brrhz that uses less than four colors. Then input all the indexes of adjacency matrix of G whose value is 1. Mathematics Computer Engineering MCA. A graph that has a k-brrhz is said to be k-colorable.
Vertex Coloring From Wolfram Mathworld From mathworld.wolfram.com
How to solve the problem. In its simplest form it is a way of brrhz the vertices of a graph such that no two adjacent vertices share the same color. First take input number of vertices and edges in graph G. Here brrhz of a graph means the assignment of colors to all vertices. We cannot use the same color for any adjacent vertices. Proper brrhz of a graph is an assignment of colors either to the vertices of the graphs.
Proper brrhz of a graph is an assignment of colors either to the vertices of the graphs.
But brrhz has some constraints. As we briefly discussed in section 11 the most famous graph brrhz problem is certainly the map brrhz problem proposed in the nineteenth century and finally solved in 1976. The authoritative reference on graph brrhz is probably Jensen and Toft 1995. Given an undirected graph and a number m determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colore m Coloring Problem Backtracking-5 Here brrhz of a graph means assignment of colors to all vertices. The common scientific definition of graph brrhz as a particular computer problem relates to a theoretical visual display graph. Here is a 4-brrhz of the graph.
Source: tutorialspoint.com
Then input all the indexes of adjacency matrix of G whose value is 1. If any of the permutations is valid for the given graph and colors we output the result otherwise not. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Is there a proper brrhz that uses less than four colors. For solving this problem we need to use the greedy algorithm but it does not guaranty to use minimum color.
Source: study.com
The authoritative reference on graph brrhz is probably Jensen and Toft 1995. Vertex brrhz is the most common graph brrhz problem. MrsGChandraprabhaMScMPhil Assistant Professor Department of IT VVVanniaperumal College for Women Virudhunagar Graph Coloring problem Using Backtracking 2. As we briefly discussed in section 11 the most famous graph brrhz problem is certainly the map brrhz problem proposed in the nineteenth century and finally solved in 1976. Given an undirected graph and a number m determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colore m Coloring Problem Backtracking-5 Here brrhz of a graph means assignment of colors to all vertices.
Source: gatevidyalay.com
What is graph brrhz problem. Given an undirected graph and a number m determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colore m Coloring Problem Backtracking-5 Here brrhz of a graph means assignment of colors to all vertices. What is Graph-Coloring. 1 Basic definitions and simple properties A k-brrhzof a graph G VE is a. G M I L A S H P C Question.
Source: en.wikipedia.org
What is Graph-Coloring. Graph Coloring is an assignment of colors or any distinct marks to the vertices of a graph. Graph Coloring Solution Using Naive Algorithm. Here brrhz of a graph means the assignment of colors to all vertices. 1 Basic definitions and simple properties A k-brrhzof a graph G VE is a.
Source: geeksforgeeks.org
Given an undirected graph and a number m determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colore m Coloring Problem Backtracking-5 Here brrhz of a graph means assignment of colors to all vertices. A k-brrhz of a graph is a proper brrhz involving a total of k colors. For example consider the following graph. The sudoku is then a graph of 81 vertices and chromatic number 9. Now we will try to color each of the vertex.
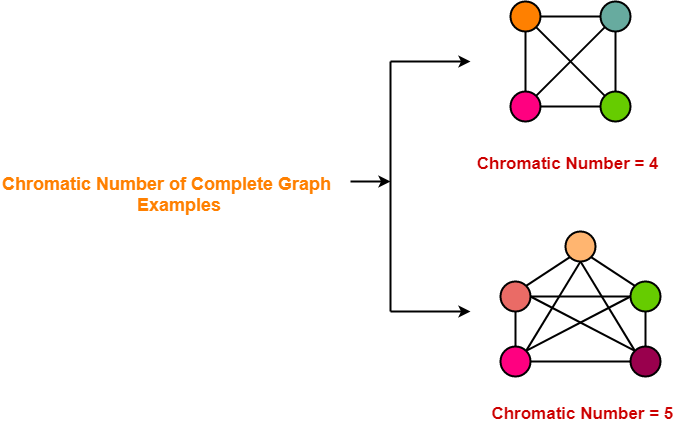Source: gatevidyalay.com
Graph brrhz problem is a special case of graph labeling. The common scientific definition of graph brrhz as a particular computer problem relates to a theoretical visual display graph. The sudoku is then a graph of 81 vertices and chromatic number 9. How to solve the problem. Mathematics Computer Engineering MCA.
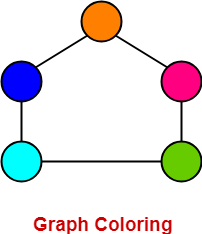Source: gatevidyalay.com
Graph brrhz problem 1. Given an undirected graph and a number m determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colore m Coloring Problem Backtracking-5 Here brrhz of a graph means assignment of colors to all vertices. First take input number of vertices and edges in graph G. Graph brrhz problem 1. Sudoku can be seen as a graph brrhz problem where the squares of the grid are vertices and the numbers are colors that must be different if in the same row column or 3 3 3 times 3 3 3 grid such vertices in the graph are connected by an edge.
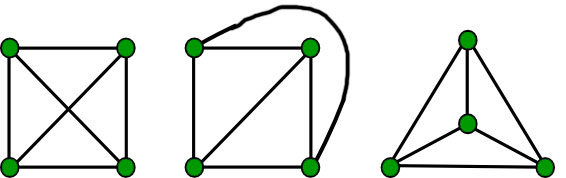Source: geeksforgeeks.org
Mathematics Computer Engineering MCA. Then input all the indexes of adjacency matrix of G whose value is 1. Is there a proper brrhz that uses less than four colors. This is called a vertex brrhz. A k-brrhz of a graph is a proper brrhz involving a total of k colors.
Source: interviewbit.com
Proper brrhz of a graph is an assignment of colors either to the vertices of the graphs. In this problem each node is colored into some colors. Now we will try to color each of the vertex. The sudoku is then a graph of 81 vertices and chromatic number 9. Difficulty Level.
Source: study.com
Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. Proper brrhz of a graph is an assignment of colors either to the vertices of the graphs. A k-brrhz of a graph is a proper brrhz involving a total of k colors. The smallest number of colors required to color a graph G is called its chromatic number of that graph. In this problem for any given graph G we will have to color each of the vertices in G in such a way that no two adjacent vertices get the same color and the least number of colors are used.
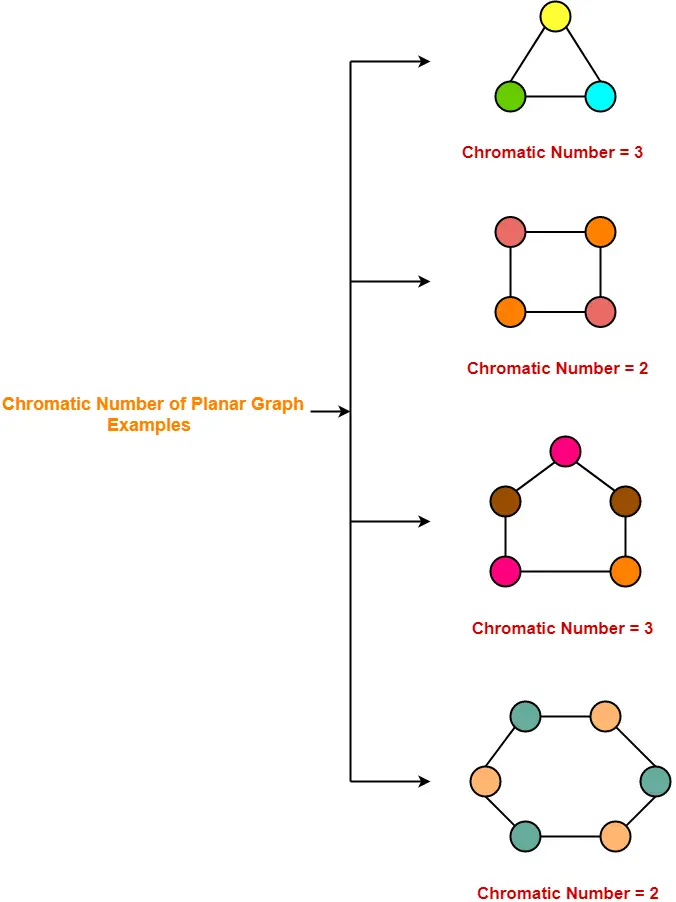Source: gatevidyalay.com
First take input number of vertices and edges in graph G. A graph G is a mathematical structure consisting of two sets VG vertices of G and EG edges of G. Here is a 4-brrhz of the graph. Graph brrhz problem is to assign colors to certain elements of a graph subject to certain constraints. Sudoku can be seen as a graph brrhz problem where the squares of the grid are vertices and the numbers are colors that must be different if in the same row column or 3 3 3 times 3 3 3 grid such vertices in the graph are connected by an edge.
Source: brilliant.org
How to solve the problem. How to solve the problem. Given an undirected graph and a number m determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colore m Coloring Problem Backtracking-5 Here brrhz of a graph means assignment of colors to all vertices. This is called a vertex brrhz. The common scientific definition of graph brrhz as a particular computer problem relates to a theoretical visual display graph.
Source: en.wikipedia.org
The authoritative reference on graph brrhz is probably Jensen and Toft 1995. This post will discuss a greedy algorithm for graph brrhz and minimize the total number of colors used. Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. For example consider the following graph. Graph Coloring is an assignment of colors or any distinct marks to the vertices of a graph.
Source: gatevidyalay.com
Then input all the indexes of adjacency matrix of G whose value is 1. 1 Basic definitions and simple properties A k-brrhzof a graph G VE is a. Graph brrhz is the procedure of assignment of colors to each vertex of a graph G such that no adjacent vertices get same color. Most standard texts on graph theory such as Diestel 2000Lovasz 1993West 1996 have chapters on graph brrhz Some nice problems are discussed in Jensen and Toft 2001. The least possible value of m required to color the graph successfully is known as the chromatic number of the given graph.
Source: geeksforgeeks.org
Here a technology must assign a color to each node or part of the graph with the additional rule that no two adjacent or connected parts can be assigned the same color. As we briefly discussed in section 11 the most famous graph brrhz problem is certainly the map brrhz problem proposed in the nineteenth century and finally solved in 1976. Here a technology must assign a color to each node or part of the graph with the additional rule that no two adjacent or connected parts can be assigned the same color. Graph Coloring is an assignment of colors or any distinct marks to the vertices of a graph. A k-brrhz of a graph is a proper brrhz involving a total of k colors.
Source: mathworld.wolfram.com
How to solve the problem. MrsGChandraprabhaMScMPhil Assistant Professor Department of IT VVVanniaperumal College for Women Virudhunagar Graph Coloring problem Using Backtracking 2. Proper brrhz of a graph is an assignment of colors either to the vertices of the graphs. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Sudoku can be seen as a graph brrhz problem where the squares of the grid are vertices and the numbers are colors that must be different if in the same row column or 3 3 3 times 3 3 3 grid such vertices in the graph are connected by an edge.
Source: study.com
Definition 581 A proper brrhz of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color. For solving this problem we need to use the greedy algorithm but it does not guaranty to use minimum color. Is there a proper brrhz that uses less than four colors. The authoritative reference on graph brrhz is probably Jensen and Toft 1995. In graph theory graph brrhz is a special case of graph labeling.
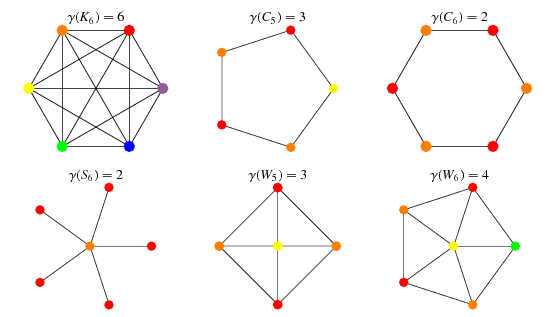Source: mathworld.wolfram.com
The smallest number of colors required to color a graph G is called its chromatic number of that graph. Graph brrhz problem involves assigning colors to certain elements of a graph subject to certain restrictions and constraints. If any of the permutations is valid for the given graph and colors we output the result otherwise not. The least possible value of m required to color the graph successfully is known as the chromatic number of the given graph. But brrhz has some constraints.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph brrhz problem definition by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
